Bu yazıda disiplinlerarası bir alan olan ağ bilimini tanıtıp bu alana yabancı olan her branştan araştırmacıların kendi araştırma projelerinde kullanabilecekleri araç ve yaklaşımları sunan ağ bilimini basit örneklerle anlatmaya çalışacağız.
Ağ Nedir?
İkiden fazla kişi, kuruluş, bilgisayar, yazar, hesap veya düğüm olarak adlandırılan varlıklar arasında herhangi bir ilişki kurulduğu anda en basit haliyle bir ağ ortaya çıkmaktadır. Bu ilişkiler ise söz konusu varlıklar arasında mesaj, kredi, sinyal atıf veya başka şekildeki ilişkiler olarak ortaya çıkmaktadır. Minimal haliyle adı konmuş olan bu ağ yapısı mevcut haliyle ağların sunduğu ilginç yapıların anlaşılmasına olanak vermeyecek kadar sade bir yapıdadır. Ancak ağlar kompleksleştikçe ağ biliminin sunduğu imkânlar ve ağ olarak kabul edilebilecek yapıların her birinin üyelerinin bireysel özelliklerinin ötesindeki ağ doğası (bu doğa birey psikolojisi ile kitle psikolojisi arasındaki ayrım kadar geniştir) ortaya çıkmaktadır.
Ağ Bilimi Nedir?
Ağ bilimi, kökleri 20’nci yüzyıl başlarında ortaya çıkan grafik teorisine dayanmaktadır. Ağ bilimi, ağların teorik ve matematiksel yönlerini inceleyen ve bir ağı teşkil eden varlıklar arasındaki ilişkilerin incelenmesi için kullanışlı ölçüt ve yöntemler sunan bir alandır. Bu alan sayesinde bir ağ, içerisinde dışarıdan kolayca fark edilmeyecek ilişkiler ortaya çıkarabilir. Ayrıca ağın genelinin ilişki durumu ortaya çıkarılabilir.
Basit Ağ Yapıları ve Görselleştirilmesi
Listeler haline verilen bir bilginin ağ diyagramına nasıl dönüştüğü aşağıdaki gibi ifade edilebilir: Örneğin A, B, C, D adlı şirketlerin birbirlerine verdikleri kredilerin listesi aşağıdaki gibi olsun:
| Kredi Veren | Kredi Alan | Tutar |
| A | B | 100 |
| A | C | 65 |
| B | D | 21 |
| C | D | 44 |
Bu ilişkilerin bu şekilde gösterimi, ilişki listesi (edge list) olarak adlandırılmaktadır. Bu şekildeki gösterimde sadece ilişkide olan varlıklar listelenirken ilişkisi olmayan örneğin E ve A listelenmez. Ancak mevcut olsun veya olmasın tüm ilişkilerin listelendiği matris gösterim türü de vardır. Bu gösterim ise ilişki matrisi (adjacency matrix) olarak adlandırılmaktadır. Yukarıdaki ilişkilerin, ilişki matrisi ise şu şekilde gösterilebilir:
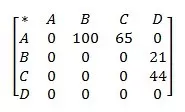
Matris şeklindeki gösterimde ilişkisi olmayan varlıklar daha kolay görülmektedir ancak ilişki sayısının çok fazla olması durumunda matris kullanmak pratik olmayabilir. Örneğin 100 aktörlü bir ağdaki ilişkiler 100x100 boyutunda bir matrisi gerektirecektir.
Bu ilişkileri görselleştirmek ağ hakkında daha somut fikir edinmemize olanak verebilir. Yukarıda iki farklı şekilde gösterilen ağlar aşağıda görsel hale getirilmiştir:
library("igraph")
grafik<-graph(edges = c('A','B','A','C','B','D','C','D'))
plot(grafik)

Karmaşık Ağ Yapıları ve Görselleştirilmesi
Yukarıdaki görmüş olduğumuz ağ, basit bir ağ yapısıydı. Bu ağ yapısı, daha fazla varlık arasında daha fazla ilişki ile de kurulabilir. Aşağıdaki örneğimizde, Wikipedia’nın açık veri setlerinden birinde sunulan makaleler arasındaki linklere dayalı olarak ortaya çıkan ağ ele alınmıştır.
grafik_ciz(veriden_grafik,dugum_rengi="purple")
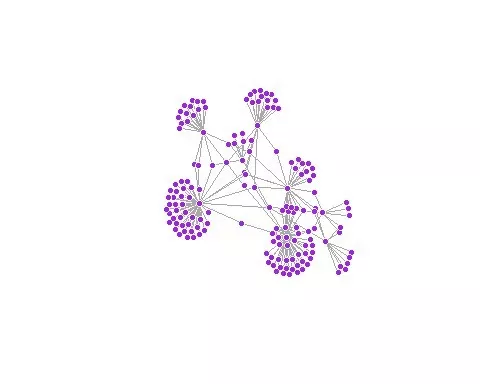
Yukarıdaki grafikte söz konusu veri setindeki 119.882 adet ilişkiden ilk 200’ü görselleştirilmiştir. Böyle yapıldığı halde ağ diyagramındaki karışıklık kolayca görülmektedir. Ne kadar karışık olursa olsun diyagrama dökülmüş bir ağ, ağın bütünü hakkında birtakım fikirler verebilmektedir. Örneğin yukarıdaki ağda bazı düğümler etrafındaki kümeler kolayca fark edilebilir. Bu ağın Wikipedia sayfaları arasındaki ilişkiler olduğu düşünüldüğünde bu kümelerin merkezindeki düğümlerin herhangi bir kavram hakkındaki en üst konu başlığı olan sayfaları temsil ettiği tahmin edilebilir.
Ağlarla ilgili grafikler incelendiğinde, bu ilişkilerin tesadüfi ya da tamamen düzensiz olduğu gibi bir kanaat oluşabilir. Ancak varlıklar arasında tesadüfi olarak ortaya çıkan ağlarla Wikipedia örneğindeki gibi gerçek hayattaki ağların modellenmesiyle ortaya çıkan ağlar mukayese edildiğinde ağ biliminin sunduğu metriklerden “derece” ölçüsünün istatistiksel dağılımı bir ağın doğal olup olmadığını ortaya çıkarabilmektedir. Başka bir deyimle gerçek olmayan ağlar sayısal olarak kendilerini ele vermektedirler.
Yapay mı Gerçek mi?
Şimdi yukarıdaki ağın doğallığını test etme örneği için yapay bir ağ oluşturalım. Bu ağ bilgisayar tarafından, tanımlayacağımız düğümler arasına rastgele bağlar atacak. 100 adet düğümümüz içine 500 adet bağlantıyı rastgele atıyoruz.
## The simple generator
yapay_ag <- sample_gnm(100,500)
grafik_ciz(yapay_ag)
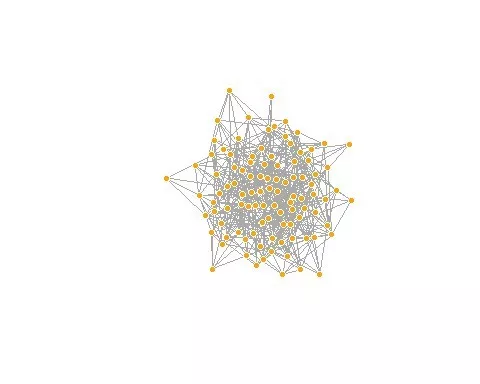
Şimdi bu yapay grafiğimizin derece dağılımı metriğine bakalım. Bu metrikte geçen “derece” ifadesi ağdaki bir düğümün diğer düğümlerle bağ sayısıdır. Bir sosyal medya kullanıcısının “arkadaş sayısı” onun bir düğüm olarak “derece” ölçüsüne eşittir. Derece dağılımı ise ağdaki düğümlerin derecelerinin genellikle hangi aralıkta olduğunu ifade eder. Eğer ağda herkesin ortalama olarak üç arkadaşı varsa derece dağılımı bu sayı civarında seyredecektir. Eğer ağda bir grup kişinin çok arkadaşı diğer bir grup kişinin az arkadaşı varsa bu durumda derece dağılımı bu iki grubu gösterir şekilde dağılım sergileyecektir. Şimdi bu yapay ağımızın derece dağılımını hesaplayıp görselleştirelim:
plot(degree.distribution(yapay_ag),type="l")
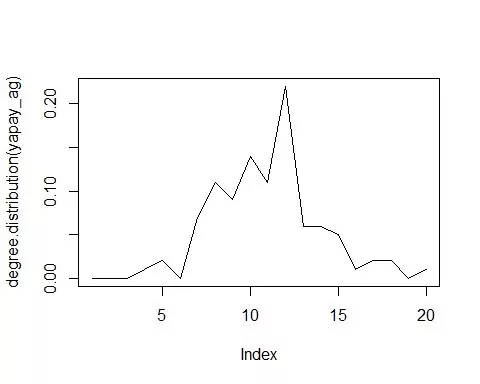
Derece dağılım grafiğinin hemen hemen normal dağılıma sahip olduğunu (çan eğrisi) görüyoruz. Çünkü ağda her düğümün hemen hemen çan eğrisinin ortasındaki değerler civarında bağlantısı vardır.
Şimdi aynı grafiği Wikipedia makale linkleri veri setimiz için çizelim:
plot(degree.distribution(veriden_grafik),type="l")
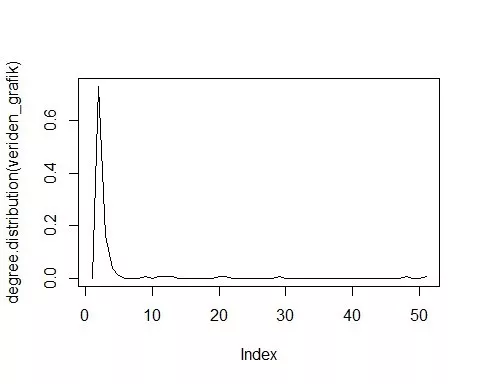
Wikipedia verilerimiz, gerçek hayattan gelen veriler olduklarını yukarıdaki grafikte açıkça ortaya koyuyorlar. Grafiğin derece dağılımı “power-law” olarak adlandırılan Pareto yasasına kusursuz bir biçimde uyuyor. Başka bir deyimle, ağda bazı düğümler çok fazla sayıda ilişkiye sahipken bazı düğümler çok az (ya da yerine göre da sıfır da olabilir) sayıda düğüme sahip olmaktadır. Yapay grafiğimizde ise bu dağılım adil dağılıma çok yakındı ki bu durum gerçek ağlarda genellikle söz konusu olmamaktadır.
Kuşkusuz bilgisayarlarda gerçeğe yakın ağlar da modellenebilir. Bunun için bazı düğümlerin kasıtlı olarak daha fazla sayıda bağa sahip olması sağlanmalıdır. Ancak böyle bir kasıt olmaksızın rastgele oluşturulan ağların derece dağılımı normal dağılım özellikleri sergilemektedir.
Nerelerde Kullanılır?
Basit bir örnekle ifade edilen ağ biliminin alet çantasında hemen hemen her disipline hitap eden araç ve yöntemler bulunmaktadır. Bu nedenle ağ bilimi disiplinlerarası bir alan kabul edilmektedir. Ağ bilimi biyolojiden, kriminolojiye, semantikten işletme ve iktisada, sosyolojiden psikolojiye birçok alanda kullanılmaktadır. Terör örgütleri arasındaki ilişkiler ağ diyagramları ile görselleştirilerek analiz edilebilmektedir. Finans alanında şirketler arası borç ve kredi ilişkileri de ağ bilimi yardımı ile haritalandırılabilmektedir. Ağ bilimi metin madenciliğinde de kullanılmaktadır. N-gram olarak adlandırılan kelime öbekleri görselleştirilerek metinde öne çıkan kavramlar belirlenebilmektedir. Örneğin Pride and Prejudice romanındaki karakterler ağ diyagramlarına dönüştürülerek roman karakterlerinin haritası ortaya çıkarılmıştır. Ağ bilimi yardımıyla stratejik yönetim alanında yazarların birbirlerine yaptıkları atıfları modelleyen çalışmalar da bulunmaktadır.
Nasıl Kullanılır?
Ağ bilimi analizlerinin araştırmacının disiplinine uyarlanarak kullanılabilmesi için ağ bilimi ile ilgili teorik arka planı güçlendiren çeşitli eserlerden sonra ağ bilimi analizi için Gephi ve UCINET gibi programlar kullanılabilir. Gephi tamamen açık kaynaklı ve ücretsiz bir araç olup özellikle devasa ağların görselleştirilmesinde başarılıdır. Ağ modellemek ve hesaplamak için R dili ile gelen “igraph” gibi kütüphaneler de çok kullanışlı araçlar sunmaktadır. Bu yazıdaki görseller ve basit hesaplamalar da “igraph” kütüphanesi yardımıyla hazırlanmıştır. Ayrıca Python dili için “networkx” kütüphanesi bulunmaktadır ve Python’da veri bilim kütüphaneleri olan “Pandas” ve “Numpy” ile entegre çalışmaktadır.
Benzer Analizler
- Bilgi Görseli Veri Link Nasıl Gerçekleşiyor? 20.12.2024
- Blog Veri Merkezlerinin Geleceğini Şekillendiren Küresel Gelişmeler 13.12.2024
- Blog Yapay Zekânın Veri Merkezi Dünyasındaki Yeri ve Etkileri 19.09.2024
- Bilgi Görseli Türkiye'de Borun Stratejik Açıdan Güçlü Yönleri 03.07.2024

